Problem 70 Hard Difficulty Find a parabola with equation $ y = ax^2 bx c $ that has slope 4 at $ x = 1, $ slope 8 at $ x = 1, $ and passes through the point (2, 15)Exploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the thirdY = ax 2 bx c or x = ay 2 by c 2 Geometric A parabola is the set of all points in a plane and a given line From the geometric point of view, the given point is the focus of the parabola and the given line is its directrix It can be shown that the line of symmetry of the parabola is the line perpendicular to the directrix through the
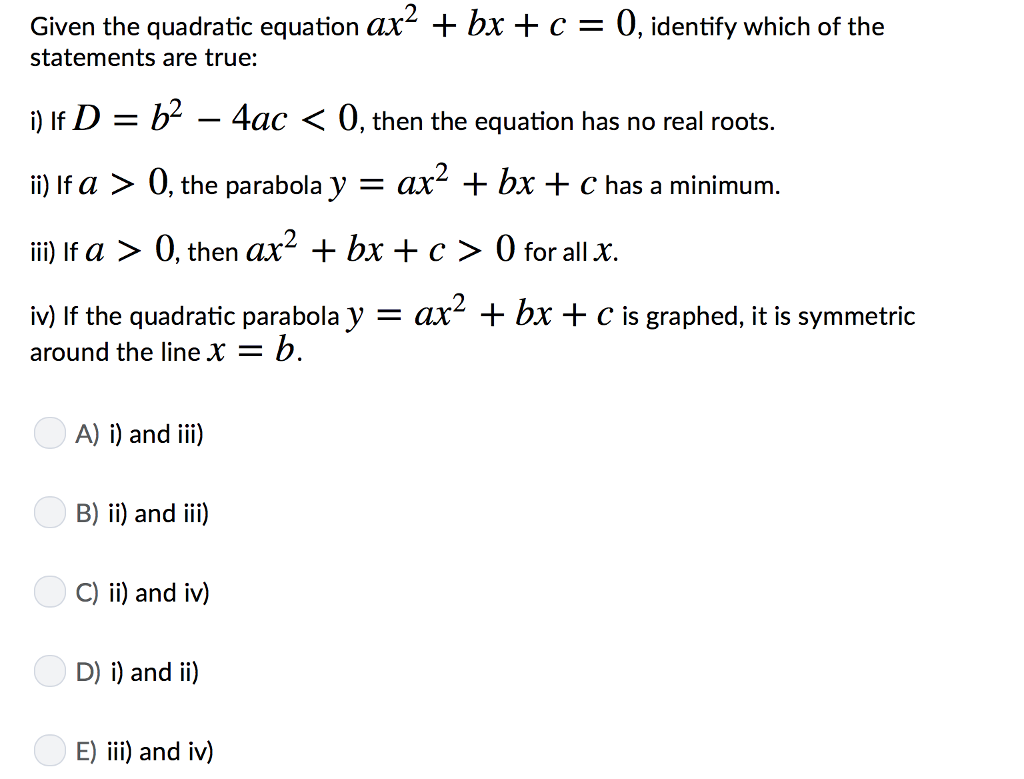
Given The Quadratic Equation Ax2 Bx C 0 Identify Chegg Com
Focus of parabola y=ax^2+bx+c
Focus of parabola y=ax^2+bx+c-Graphs of quadratic functions All quadratic functions have the same type of curved graphs with a line of symmetry The graph of the quadratic function \(y = ax^2 bx cY = ax 2 bx c The cvalue is the yvalue in the yinterception In the equation of a vertical parabola the cvalue is the distance from the focus to the vertex and from the vertex to the directrix H and k are the vertex and when the center is at




Graphing Y Ax 2 Bx C
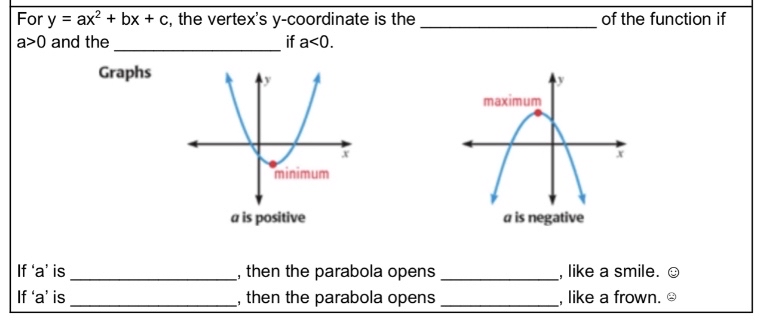
One formula works when the parabola's equation is in vertex form and the other works when the parabola's equation is in standard form Standard Form If your equation is in the standard form $$ y = ax^2 bx c $$ , then the formula for the axis of symmetry is $ \red{ \boxed{ x = \frac {b}{ 2a} }} $ Vertex Form If yourWhat are the coefficients a, b, and c of the parabola y = ax^2 bx c that passes through the point (3, 13) and tangent to the line 8x y = 15 at (2, 1)? A parabola y = ax 2 bx c crosses the x axis at (α, 0) (β, 0) both to the right of the origin A circle also passes through these two points A circle also passes through these two points The length of a tangent from the origin to the circle is
Y= ax^2 bx c = (4 3^05)*x^2 (4 2*(3^05))*x 4 b) y= ax^2 bx c has vertex (4,1) and passes through (1,11) 1 = 16a 4b c 11 = a b c the vertex is x = b/2a that is b/2a = 4 by solving the system of equations 16a 4b c = 1 a b c = 11b/2a = 4 we find a = 04 b = 32 c = 74 the equation of the quadratic That means that the points on the parabola, when plugged into the equation, make a true statement, and conversely, the only points that can be plugged in to make the equation true are points on the parabola The farther an x value is from the parabola's apex x0, the higher is its y value when a is positive and the lower its y value when a is negative x1 x0 > x2 x0 && a > 0 > y1 > y2 x1 x0 > x2 x0 && a < 0 > y1 < y2 When a is zero, your parabola is really a line and the x values are already sorted in the correct order when b is positive or in the reverse order when b is negative
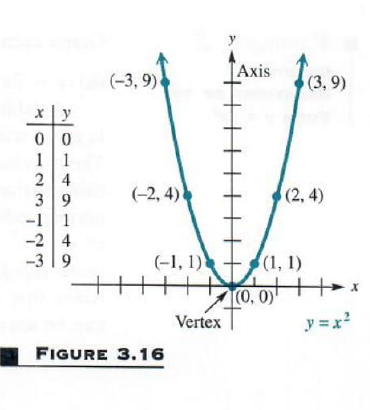
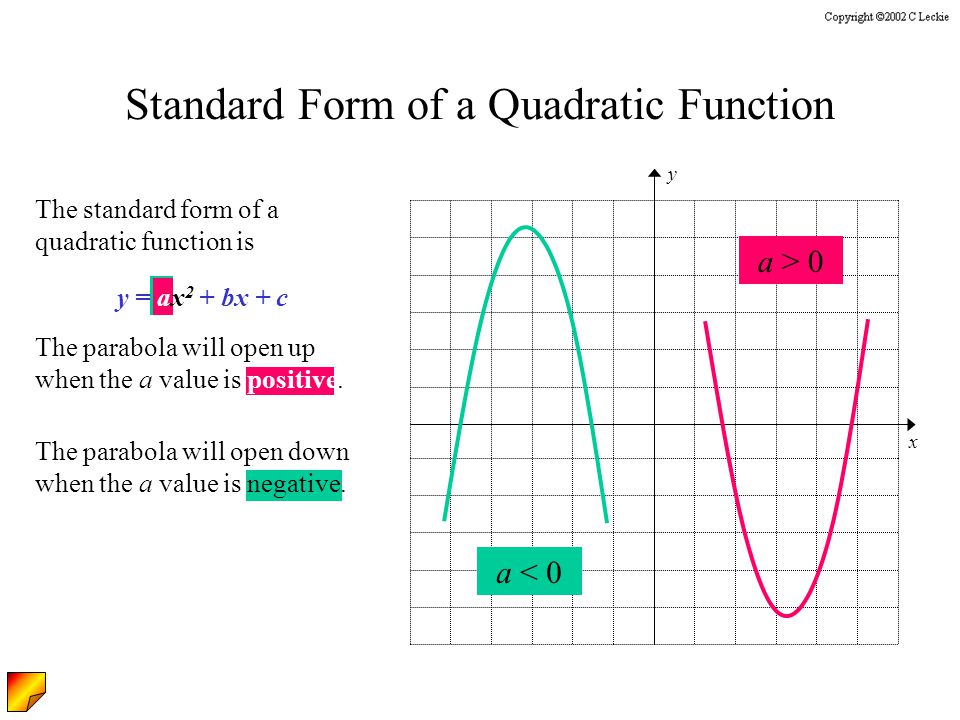
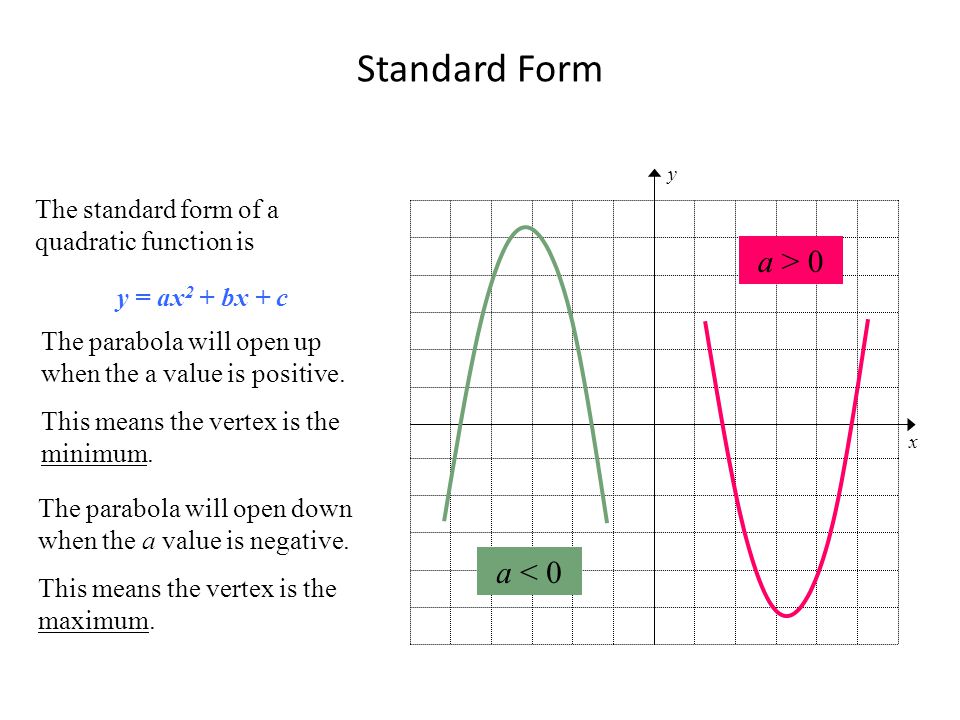
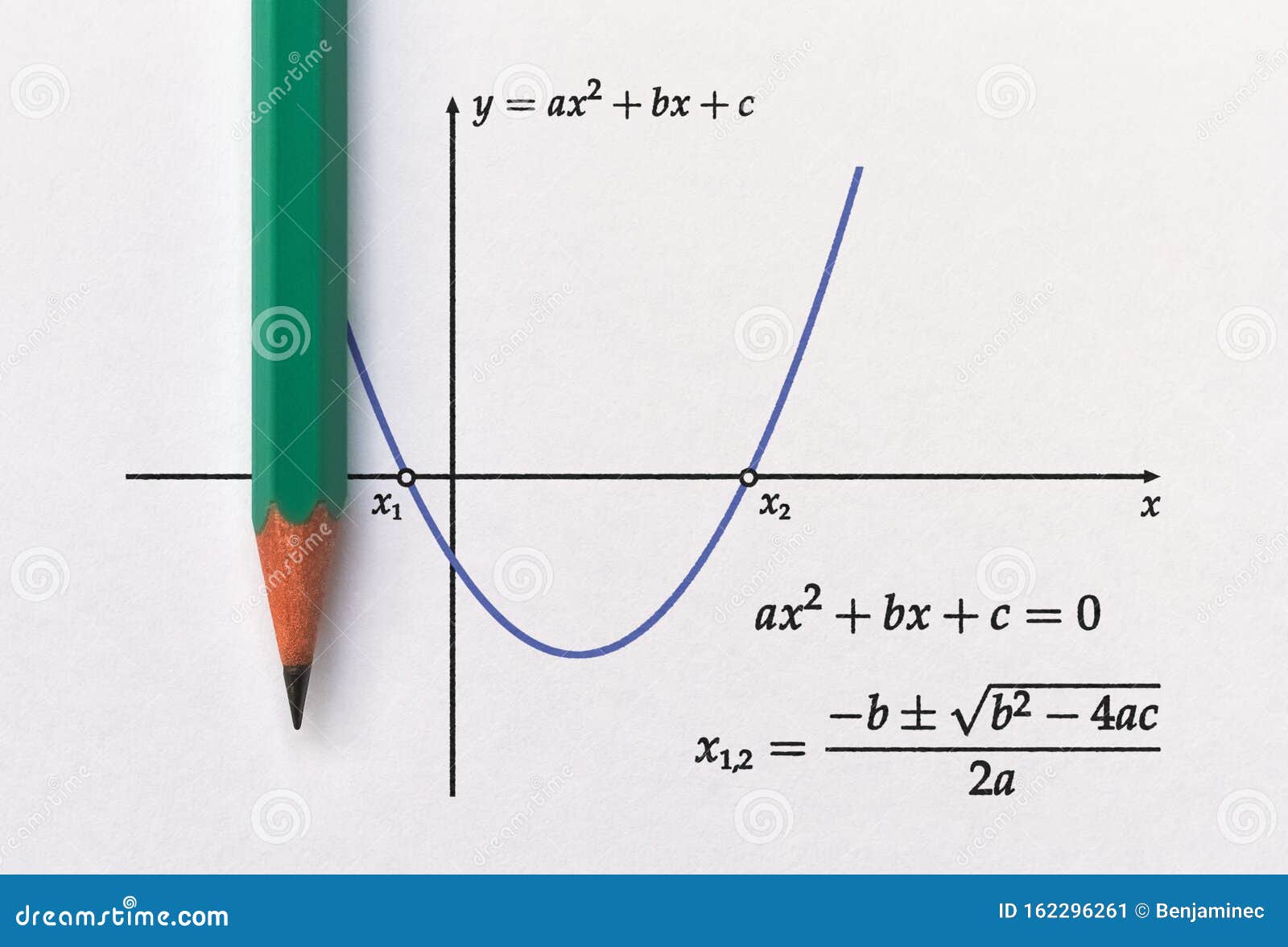
The parabola y=ax^2bxc is graphed belowC = st Partial factored form y = x(ax b) c Factored form y = a(xs)(xt) zeros x = s;The Graph of y = ax2 bx c 393 Lesson 64 The Graph of y = ax2 bx c Lesson 6–4 2 BIG IDEA The graph of y = ax bx c, a ≠ 0, is a parabola that opens upward if a > 0 and downward if a < 0 Standard Form for the Equation of a Parabola



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau



Answered For Y Ax Bx C The Vertex S Bartleby
Pembahasan Soal Parabola dengan puncak dapat dikonstruksi dengan y = ax 2 bx c Karena parabola melalui titik (0,p), maka Jadi, dengan mengidentikkan terhadap bentuk y = ax 2 bx c maka nilai b = 4 Pembahasan terverifikasi oleh RoboguruParábola y=ax^2bxc Parábola y=ax^2bxc Comprueba como varía su gráfica al variar los valores de a, b y c con los deslizadoresX = t Vertex form y = a(x – h) 2 k 1 < 1 > a < 1 parabola stretched by a h (vertex) > 0 moves parabola right h units h (vertex) < 0 moves parabola
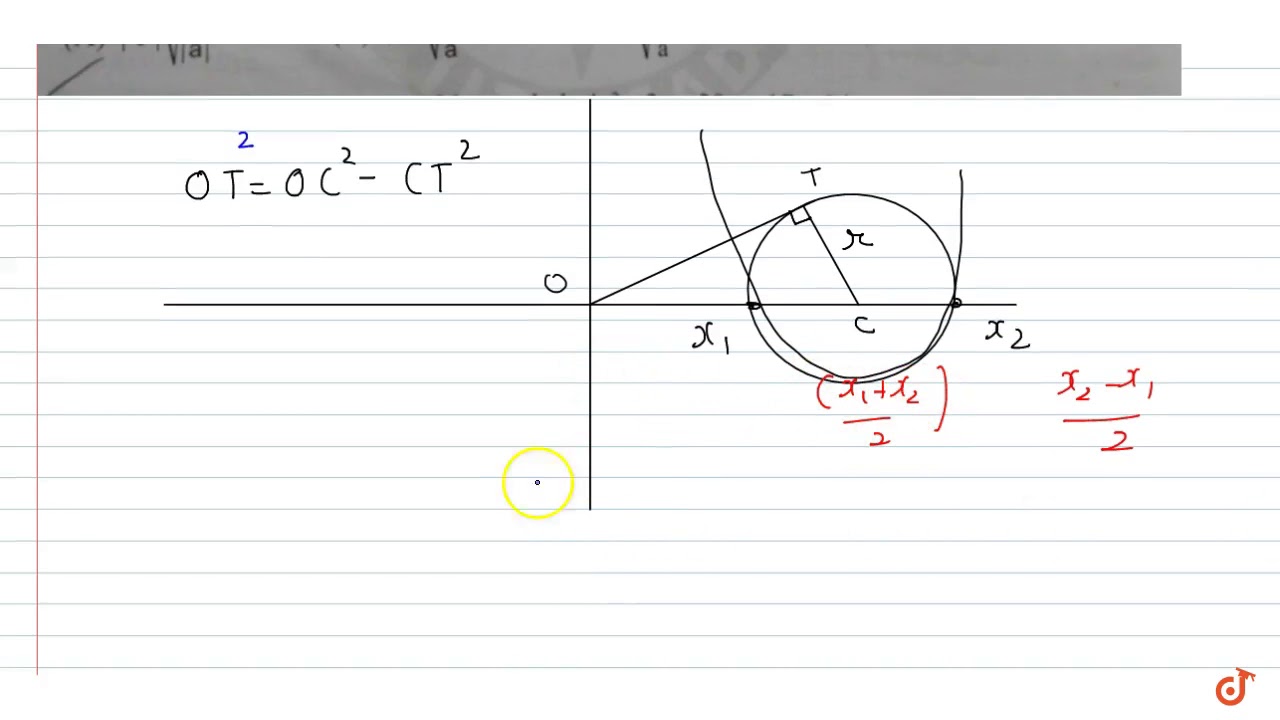



A Parabola Y Ax 2 Bx C Ac Gt 0 Crosses The X Axis At A And B A Variable Circle Is Dra Youtube




Graphing Y Ax 2 Bx C
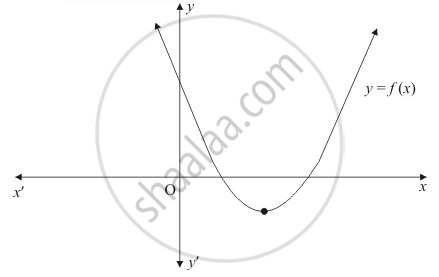
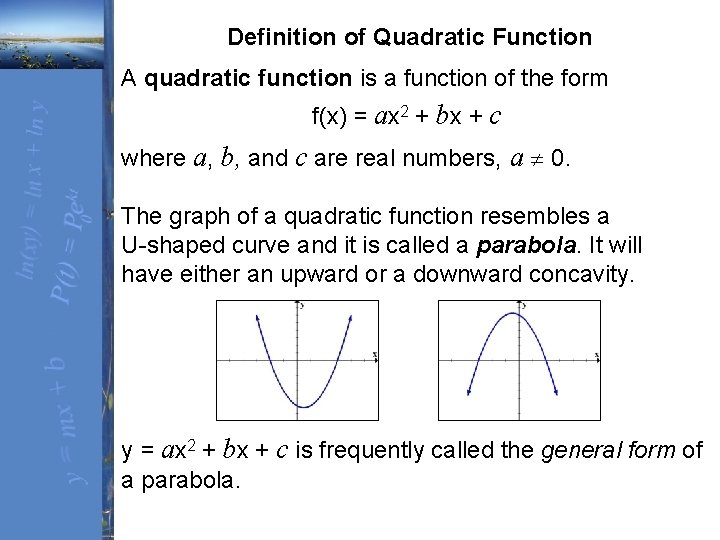
Given a quadratic function \(f(x) = ax^2bxc\), it is described by its curve \y = ax^2bxc\ This type of curve is known as a parabola A typical parabola is shown here Parabola,About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators Starting from scratch, suppose we want to construct an upward or downward opening parabola (ie, one of the form $y = ax^2 bx c$) Let its vertex be $(h, k)$ The definition of a parabola is that it is the set of all points equidistant to



What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora



The Graph Of The Polynomial F X Ax2 Bx C Is As Shown Below Fig 2 19 Write The Signs Of A And B2 4ac Mathematics Shaalaa Com
College Algebra Find the standard form of the equation of the parabola with the given characteristics and vertex at the originExploring Parabolas By Joshua Singer Most of us are aware that the quadratic equation yields the graph of a parabola We are going to explore how each of the variables a, b, and c affect the graph of First, let's take a look at the simplest of the quadratic equation , where a = 1, b = 0, and c = 0 This gives us the quadratic equation Find the equation of the parabola y = ax2 bx c that passes through the points To verify your result, use a graphing utility to plot the points and graph the parabola (−2, −15), (−1, −4), (1/2,10) y=?




Quadratic Formula Wikipedia




Graph Of Y Ax 2 Bx C Novocom Top
A parabola y = ax^2 bx c crosses the x axis at (alpha, 0) (beta, 0) both to the right of the origin A circle also passes through these two points The length of We learned from the video lesson that the b value in the quadratic equation y = ax2 bx c affects the location of the parabola Each parabola has the same a value Each parabola has the same a value2 days ago The graph of any quadratic equation \(y=ax^{2}bxc\), where a, b, and c are real numbers and a≠0, is called a parabola When graphing parabolas, find the vertex and y intercept If the x intercepts exist, find those as well



1
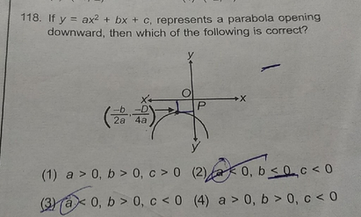



118 If Y Ax2 Bx C Represents A Parabola Opening Downward Scholr
This is your generic quadratic equation y = ax 2 bx c Move the loose number over to the other side y – c = ax 2 bx Factor out whatever is multiplied on the squared term Make room on the lefthand side, and put a copy of "a" in front of this space Graph of a quadratic function As said before, the graph of a quadratic function is known as a parabola Having calculated the roots, the vertex and the yinterception, one can now plot the graph The graph of the function in the previous example is f (x) = x 2 – 5x 6 Plotting the graph of a quadratic function y = ax 2 bx c, one will Find abc if the graph of the equation y=ax^2bxc is a parabola with vertex (5,3), vertical axis of symmetry, and contains the point (2,0)



Math Spoken Here About Quadratics 3



Parabola
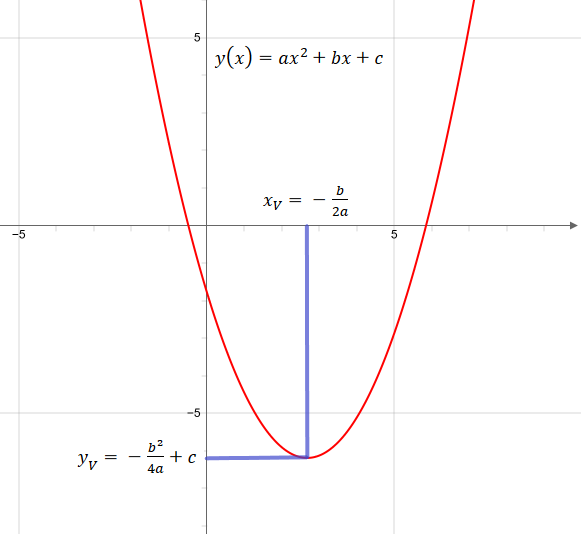
The parabola has the equation y=2x^2x If y=ax^2bx then y'=2axb This gives us our slope of y at any given x So at the point (1,1), the slope must be y'=2a(1)b=2ab We know the slope must also be 3 at the point (1,1), to match the linear equation given Thus, these two slope values must be equal 2ab=3 1 We also know that (1,1) is a point on the parabola, so it mustThis problem has been solved!To Graph the Quadratic Function \(y = ax^2 bx c\text{}\) Determine whether the parabola opens upward (if \(a \gt 0\)) or downward (if \(a \lt 0\)) Locate the vertex of the parabola The \(x\)coordinate of the vertex is \(x_v =\dfrac{b}{2a}\text{}\) Find the \(y\)coordinate of the vertex by substituting \(x_v\) into the equation of the parabola



How To Show That The Vertex Of The Parabola Math Y Ax 2 Bx C Math Can Be Expressed As Math B 2a C B 2 4a Math Quora
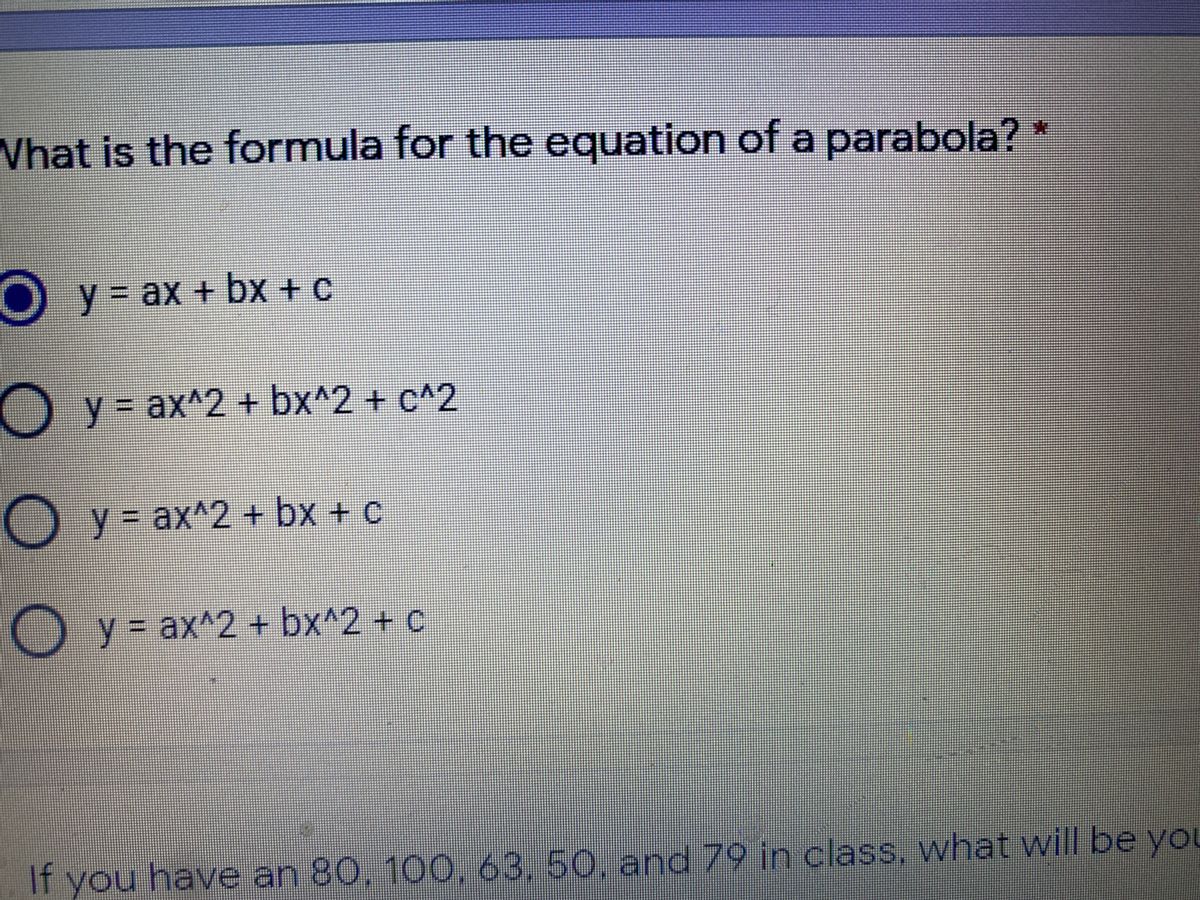



Answered Hat Is The Formula For The Equation Of Bartleby
This video discusses the techniques of graphing quadratic functions in the form y = ax^2 bx c using table of values We will use a formula to fiQuestion 2519 A parabola y = ax^2 bx c has vertex (4, 2) If (2, 0) is on the parabola, then find the value of abc If (2, 0) is on the parabola, then find the value of abc Answer by Fombitz() ( Show Source )The general form of a quadratic is "y = ax 2 bx c"For graphing, the leading coefficient "a" indicates how "fat" or how "skinny" the parabola will beFor a > 1 (such as a = 3 or a = –4), the parabola will be "skinny", because it grows more quickly (three times as fast or four times as fast, respectively, in the case of our sample values



Lessons 5




Focus Of Parabola Y Ax 2 Bx C Is
a parabola y=ax2bxc with axis of symmetry x=c intersects a straight line y=axb at two points, the vertex of the parabola V(c,d) and anothe point W Find a set of numbers a,b,c (not 0) that satisfy this situation Show that there are more than one set of numbers that satisfy this situation and estmate how many there areBxc=yax^{2} b x c = y − a x 2 Sottrai c da entrambi i lati With the right parameters it could actually be any line that crosses the given parabola and not parallel to the axis I think I know what you are talking about But it is not a uniquely defined line With the right parameters it could actually be any line that crossesBy = ax c divide both sides of this equation by b to get y = (a/b)*x (c/a) your slope of m is equal to (a/b) your yintercept of b is equal to (c/a) no relationship between b in the slopeintercept form of the equation to the b which is the coefficient of the x term



Solution A Parabola Y Ax 2 Bx C Has Vertex 4 2 If 2 0 Is On The Parabola Then Find The Value Of Abc



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
If y=ax^(2)bxc is the reflection of parabola y=x^(2)4x1 about the line y=3,abc= The locus of the middle points of all chords of the parabola y^(2)=4ax passing through the vertex is y=a(x2)(x4) In the quadratic equation above, a is a nonzero constantParabola satisfies (3, 13) and (2, 1) 9a 3b c = 13 and 4a 2b c = 1 Subtracting these gives 5a b = 12 Eqn A y'(2) = slope of tangent line = 8 y' = 2ax b, y'(2) = 4a b = 8 Eqn BGeometrically, these roots represent the xvalues at which any parabola, explicitly given as y = ax 2 bx c, crosses the xaxis As well as being a formula that yields the zeros of any parabola, the quadratic formula can also be used to identify the axis of symmetry of the parabola, and the number of real zeros the quadratic equation contains
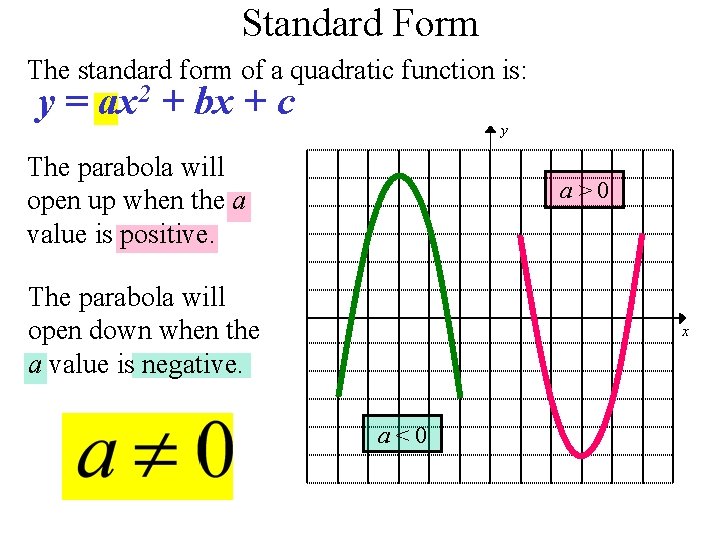



Quadratic Function Y Ax 2 Bx C Quadratic



If Y Ax 2 Bx C Represents A Parabola With Vertex A As Shown In The Figure And B 2 2 B 2ac Sarthaks Econnect Largest Online Education Community
Now substitute #a=3 # and #b=2# in the equation #y=ax^2bxc# #y=3x^22xc# We have to find the value of #c# We know the parabola is passing through the point #2,15# We shall use this information to find the value of #c# #3(2)^22(2)c=15# #124c=15# #8c=15# #c=158=7# #c=7# Now substitute #a=3 #, #b=2# and #c=7# in the equation #y=ax^2Quadraticequationcalculator ax^2bxc=0 en Related Symbolab blog posts High School Math Solutions – Quadratic Equations Calculator, Part 2 Solving quadratics by factorizing (link to previous post) usually works just fine But what if the quadratic equationQUADRATIC RELATIONS Standard form y = ax 2 bx c b = (s t);




Y Ax2 Bx C Graph Novocom Top



Modelli Algebrici Geometrici
1 Explain why the condition a ≠ 0 must be stated to ensure that y = ax^2 bx c is a quadratic relation 2 Two parabolas have the same xintercepts, (0, 0) and (10, 0) One parabola has a maximum value of 2 The other parabola has a minimum value of 4 Sketch the graphs of the parabolas on the same axesYour equation will have the formula y = Ax^2 Bx C (writing it as Ax^2 Bx C = y may help your math) Your three (x, y) points can be plugged into this formula to to get a system of three equations in A, B, and C, which can be solved by substitution or elimination to obtain A, B, and C 1 Answer The parabola equation is y=ax^2bxc The point (1,3) passes through parabola so it satisfy the curve The tangent point will also satisfy the parabola So (2,1) will satisfy the curve To find out the tangent , equate the first derivative at (2,1)




2 1 Graphing Quadratic Functions Quadratics Exploration




Quadratic Equation Handwiki
answered by SudhirMandal (535k points) selected by faiz Best answer We have Therefore, the vertex (X = 0, Y= 0) is given by (b/2a, 4ac b2/4a) The focus ( X = 0,Y =1/4a) is given by The directrix equation is given by Y = 1/4a or y = 4ac b2/4aThe graph of a quadratic equation in two variables (y = ax2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot We say that the first parabola opens upwards (is a U shape) and the second parabola opensSee the answer Find a parabola with equation y = ax 2 bx c that has slope 13 at x = 1, slope −23 at x = −1, and passes through the point (2, 34)




Classzone Chapter 4



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
Click here👆to get an answer to your question ️ The graph of the equation y = ax^2 bx c has shape open upwards like which is known as parabola, when Join / Login maths The graph of the equation y = a x 2 b x c has shape open upwards like which is known as parabola,
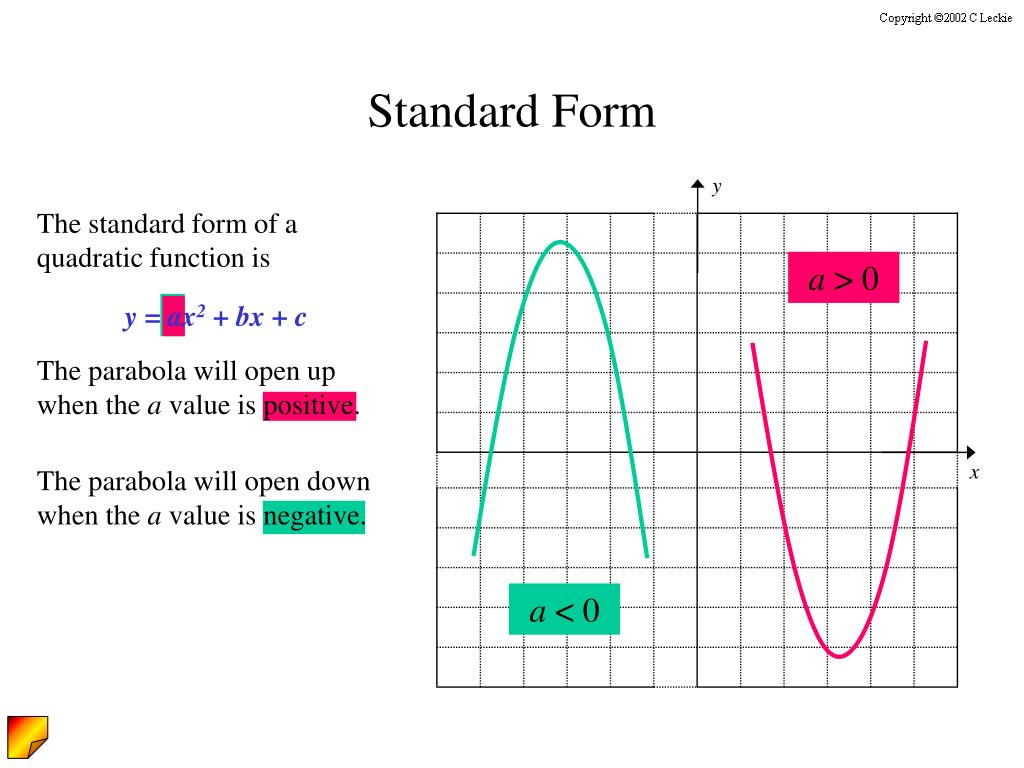



Ppt Graphing Quadratic Functions Powerpoint Presentation Free Download Id



Solve Quadratic Relation Parabolas Step By Step Math Problem Solver
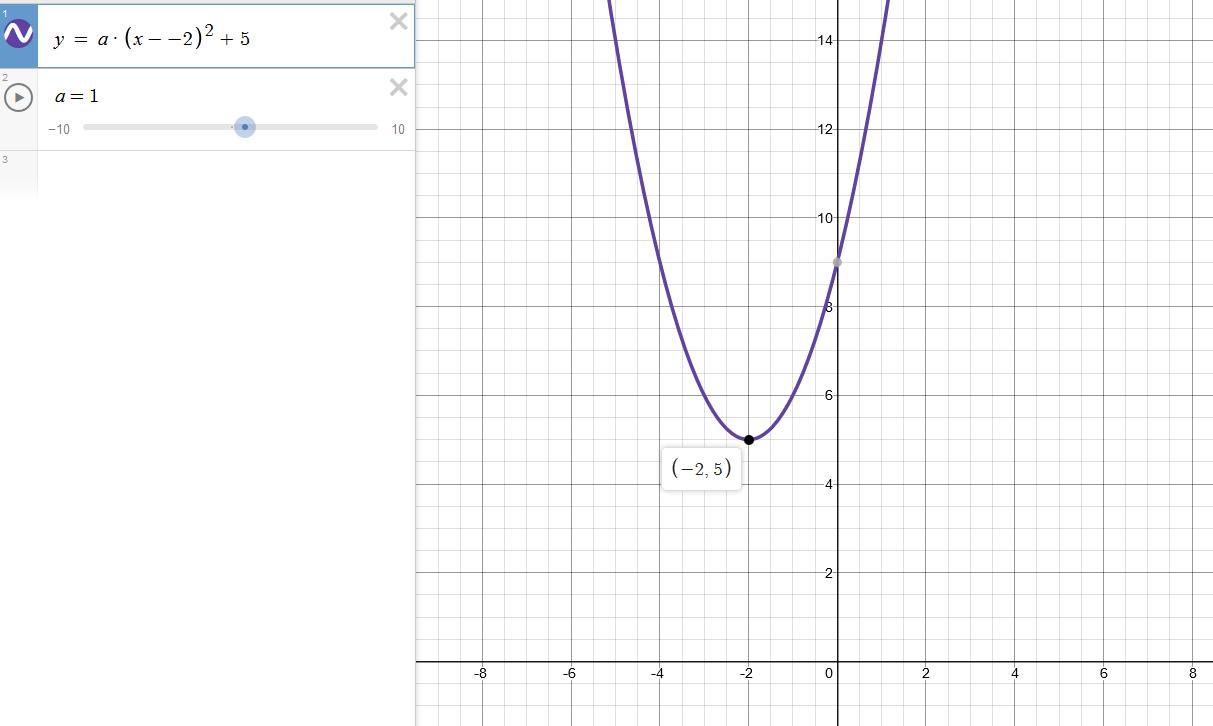



The Graph Of Y Ax 2 Bx C Is A Parabola That Opens Up And Has A Vertex At 2 5 What Is The Solution Set Of The Related



Quadratic Graph Example Y Ax Expii
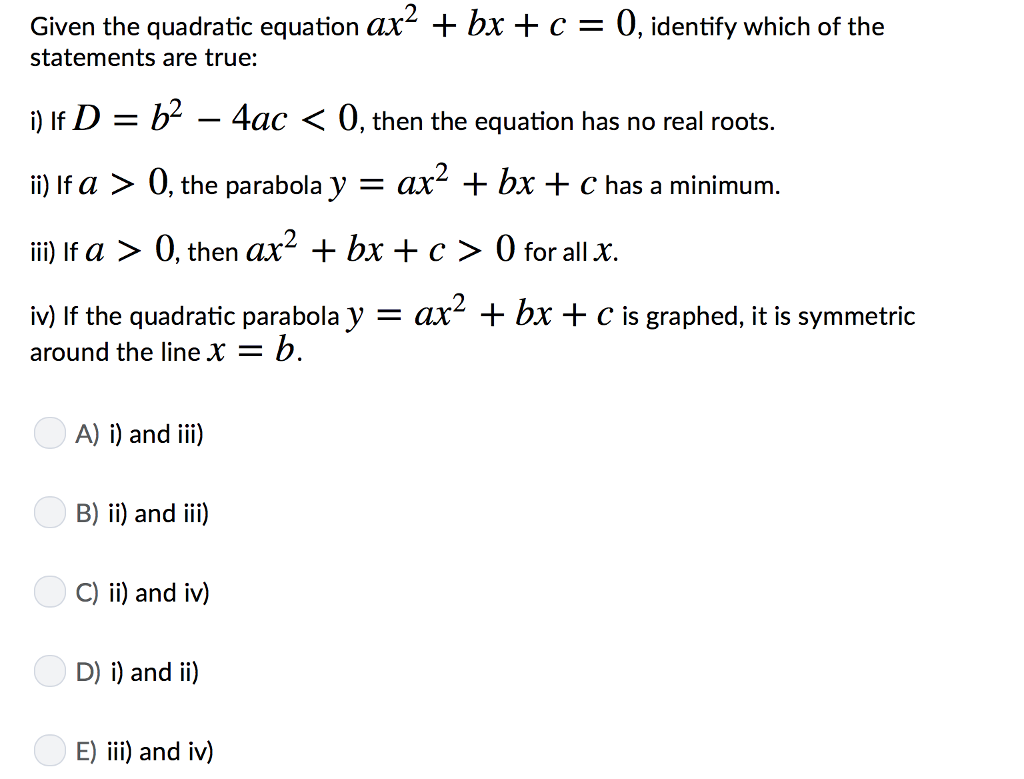



Given The Quadratic Equation Ax2 Bx C 0 Identify Chegg Com




Graphing Parabolas




A Parabola Y Ax2 Bx C Has A Y Intercept Of 5 And P Gauthmath
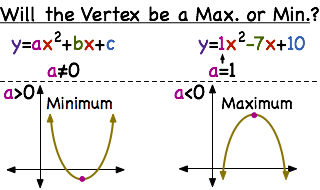



How Do You Determine If The Vertex Will Be A Maximum Or Minimum Printable Summary Virtual Nerd
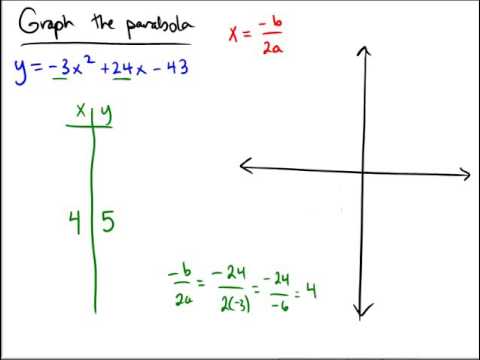



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube



Quadratics



Sat Math Grid Ins Question 97 Answer And Explanation Cracksat Net



Assignment 2
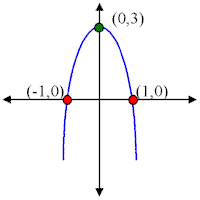



Parabolas




Parabola Y Ax2 Bx C Melalui 3 8 Yang Menyinggung Garis 4x Y 4 Di Titik 1 8 Mas Dayat



Quadratic Function Y Ax2 Bx C When A Is Sutori



Unique Quadratic Equation In The Form Y Ax 2 Bx C



Vertex And Intercepts



Online Calculator For Converting Quadratic Equation From Normal Form To Vertex Form



Graphing Quadratic Functions Y 2 Ax Bx C



Quadratic Graph Example Y Ax C Expii



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora



Lessons 5
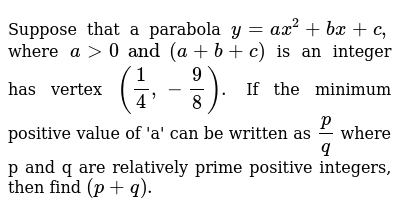



Suppose That A Parabola Y Ax 2 Bx C Where A 0 And A B C Is An Integer Has Vertex 1 4 9 8 If The Minimum Positive Value Of A




1 The Standard Form Of A Quadratic Equation Is Y Ax 2 Bx C 2 The Graph Of A Quadratic Equation Is A Parabola 3 When A Is Positive The Graph Opens Ppt Download
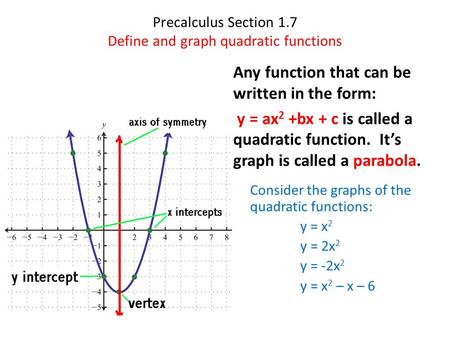



9 3 Graphing Y Ax Bx C 2 1a Y X 1 For 3 X 3 2 X Y B Does It Open Up Or Down C Identify The Axis Of Symmetry And Its Vertex Ppt Download
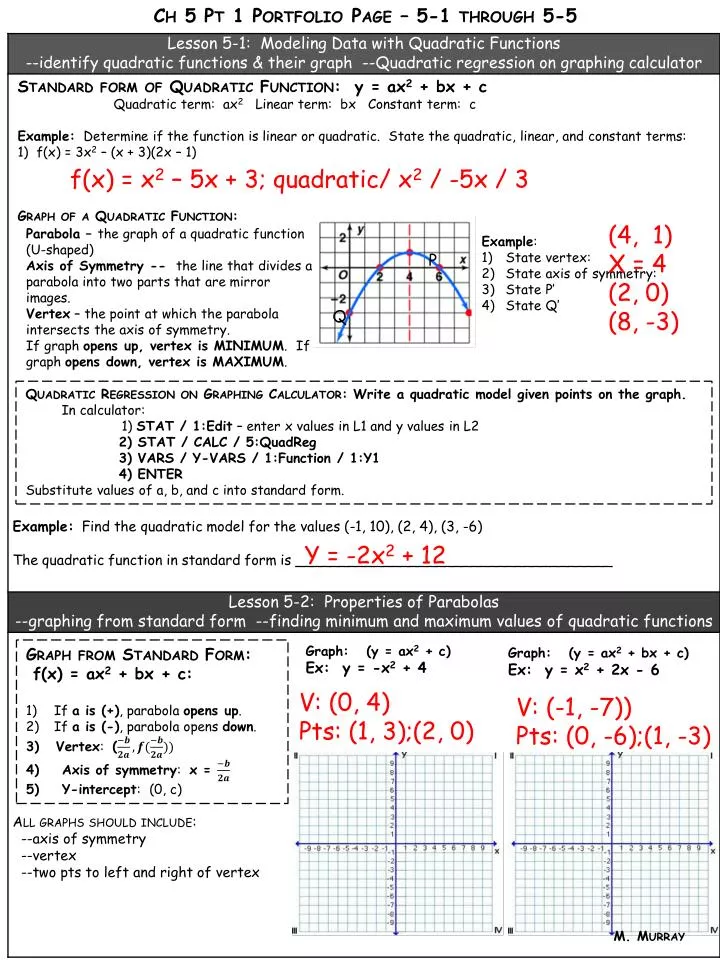



Ppt Standard Form Of Quadratic Function Y Ax 2 Bx C Powerpoint Presentation Id




The Given Figure Shows The Graph Of The Polynomial F X Ax 2 Bx C Then Ltbr Gt 1 Nbsp Youtube
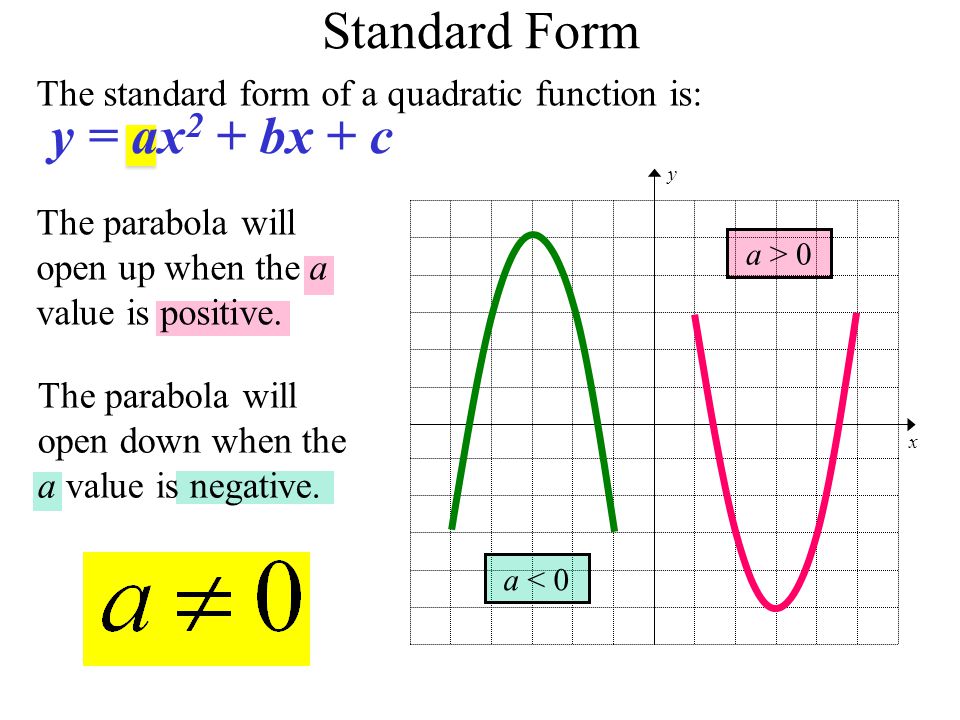



Graphing Quadratic Functions Ppt Video Online Download
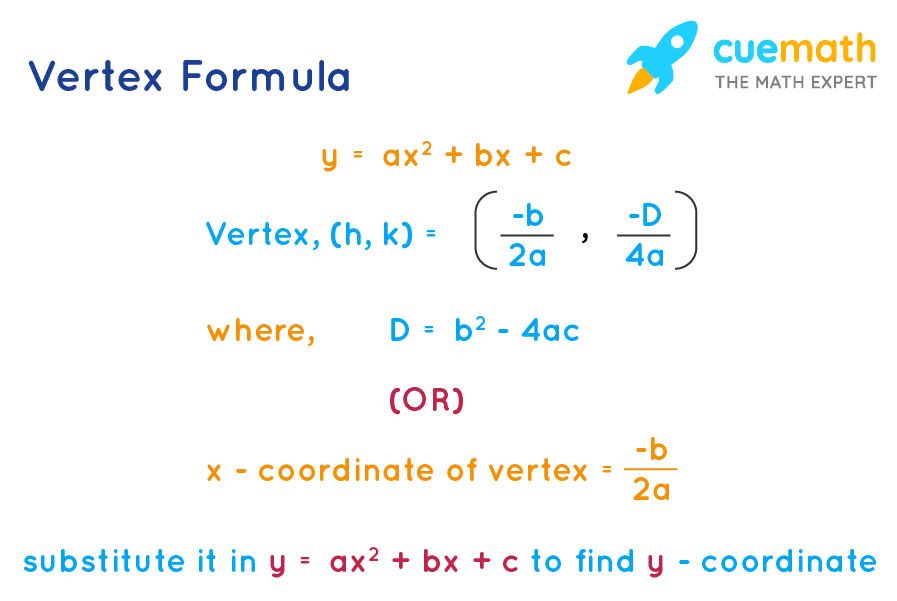



Vertex Formula What Is Vertex Formula Examples




Which Of The Following Is An Equation In The Form Y Ax2 Bx C Of The Parabola Shown In The Brainly Com
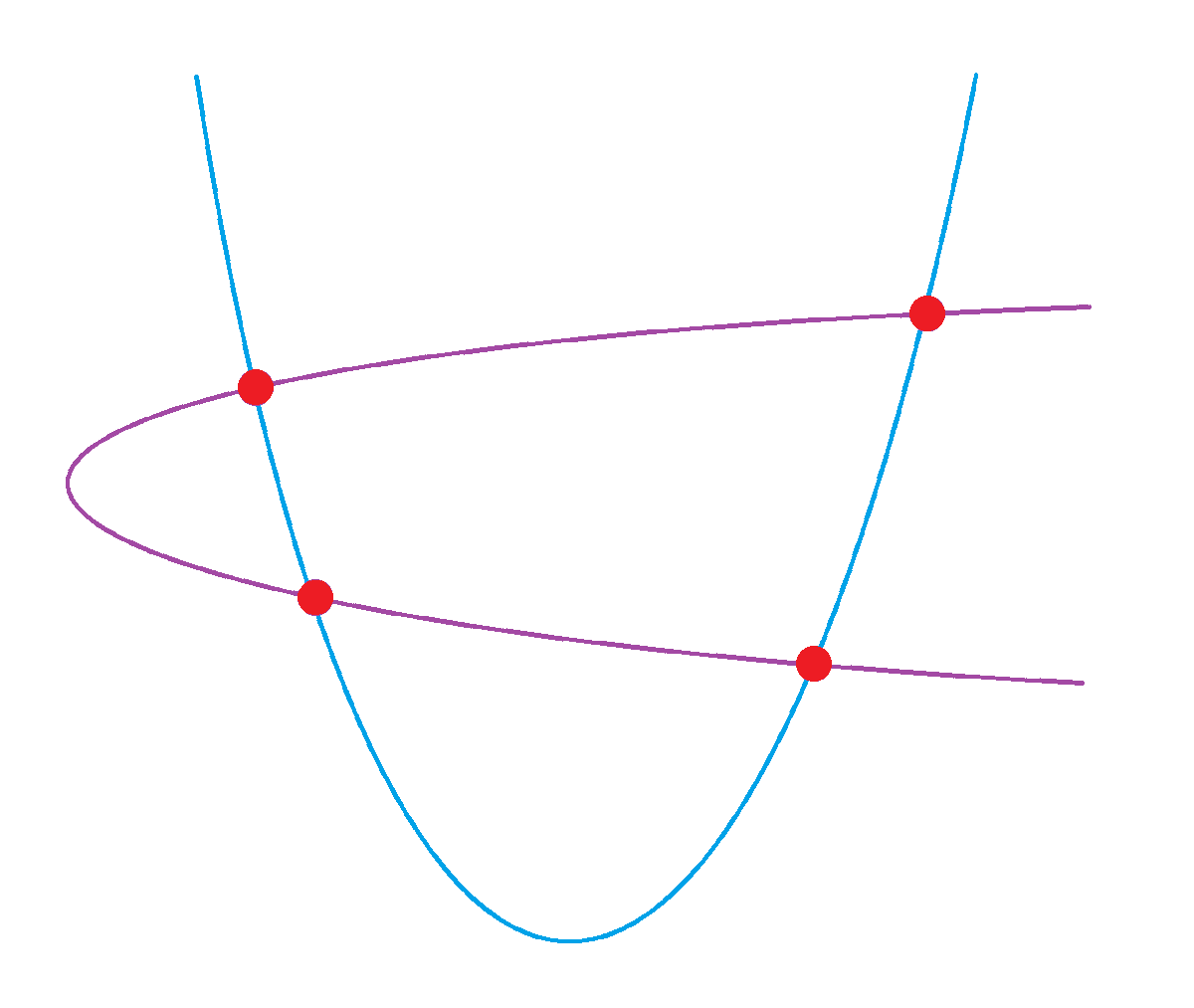



James Tanton Consider The Four Intersection Points Of Two Intersecting Parabolas Y Ax 2 Bx C And X Y 2 Dy E They Lie On A Circle What Is The Equation Of The That Circle T Co V2saijpuem




Graphing Y Ax 2 Bx C



Standard Form
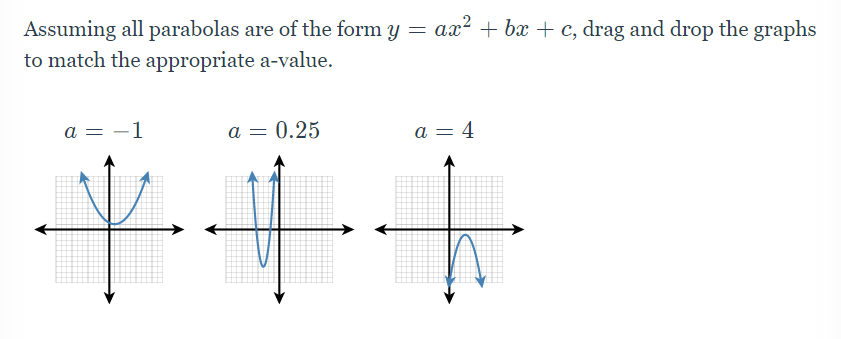



Answered Assuming All Parabolas Are Of The Form Bartleby
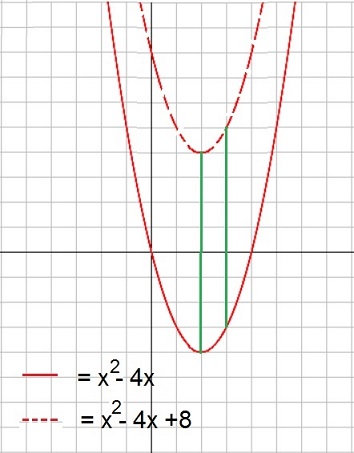



Albert Van Der Sel Polynomials
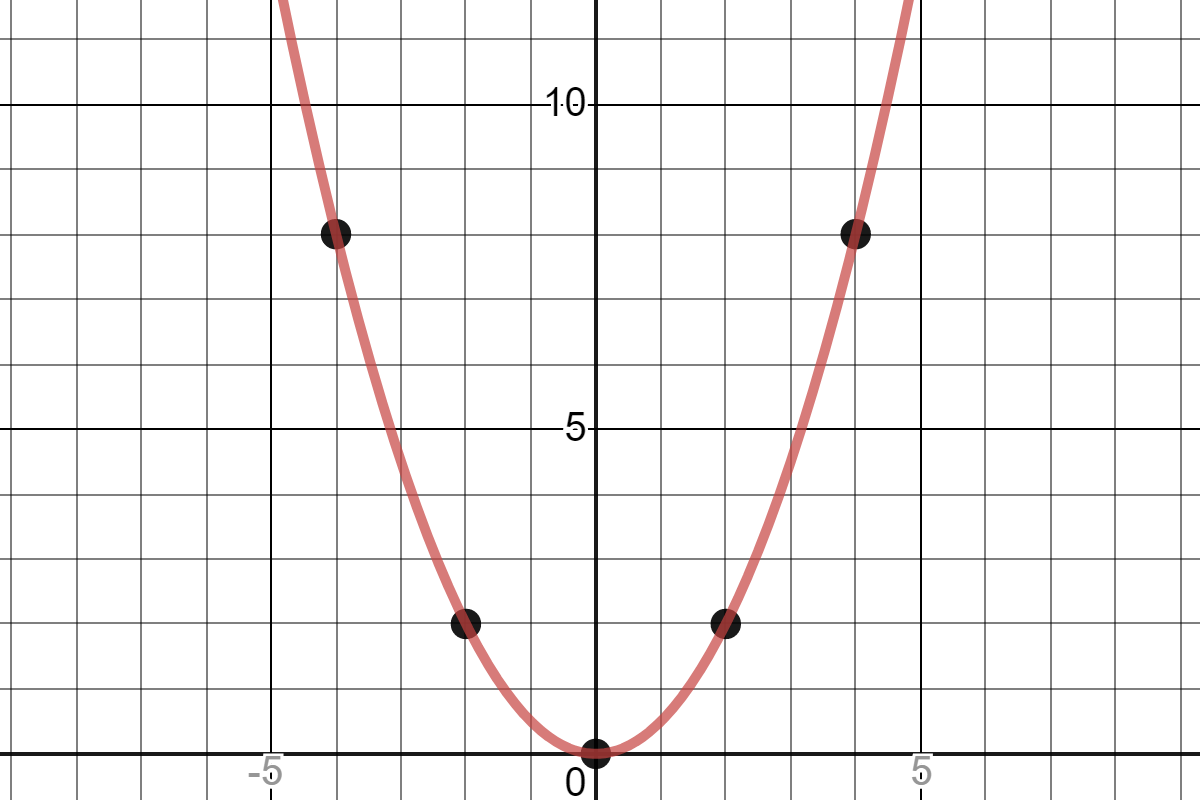



Quadratic Graph Example Y Ax Expii




Graphing Y Ax2 Bx C Youtube



A Tangent To A Quadratic
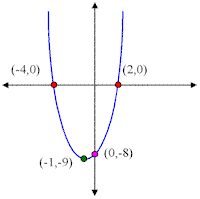



Parabolas




How To Graph Y Ax 2 Bx C Novocom Top
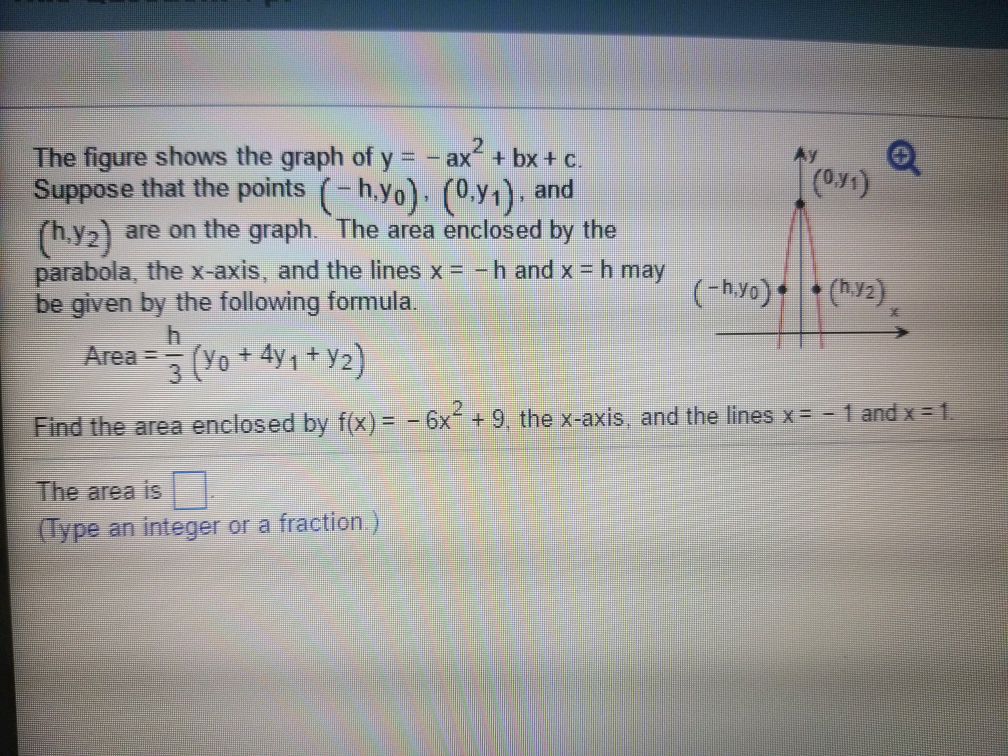



The Figure Shows The Graph Of Y Ax 2 Bx C Chegg Com



Graphing Quadratic Functions Y Ax 2 Bx C




Consider The General Quadratic Function F X Ax 2 Bx C With A Is Not Equal To 0 A Find The Coordinates Of The Vertex In Terms Of A B And




Quadratic Function




Quadratic Function Honors Physics 15



15 04 Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube




Quadratic Systems A Line And A Parabola Video Khan Academy



Graph Parabola Quadratic Function Roots Solution Stock Photo Edit Now




Parabola Y Ax2 Bx C Melalui 3 8 Yang Menyinggung Garis 4x Y 4 Di Titik 1 8 Mas Dayat
%20of%20a%20parabola%201.gif)



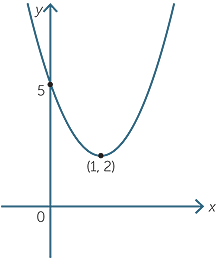
Finding The Y Intercepts Of A Parabola



Exploring Parabolas Y Ax 2 Bx C



Transformations Of Equations Of Parabola Parametric Equations Of Parabola




This Is What The Problem Says Assuming All Parabolas Are Of The Form Y Ax 2 Bx C Drag And Drop The Brainly Com



Exploring Parabolas Y Ax 2 Bx C



Lesson 10 2 Quadratic Functions And Their Graphs Y Ax 2 Bx C Ppt Download



Given A Parabola Having Equation Y Ax 2 Bx C With A 0 What Are The Coordinates Of The Vertex Quora
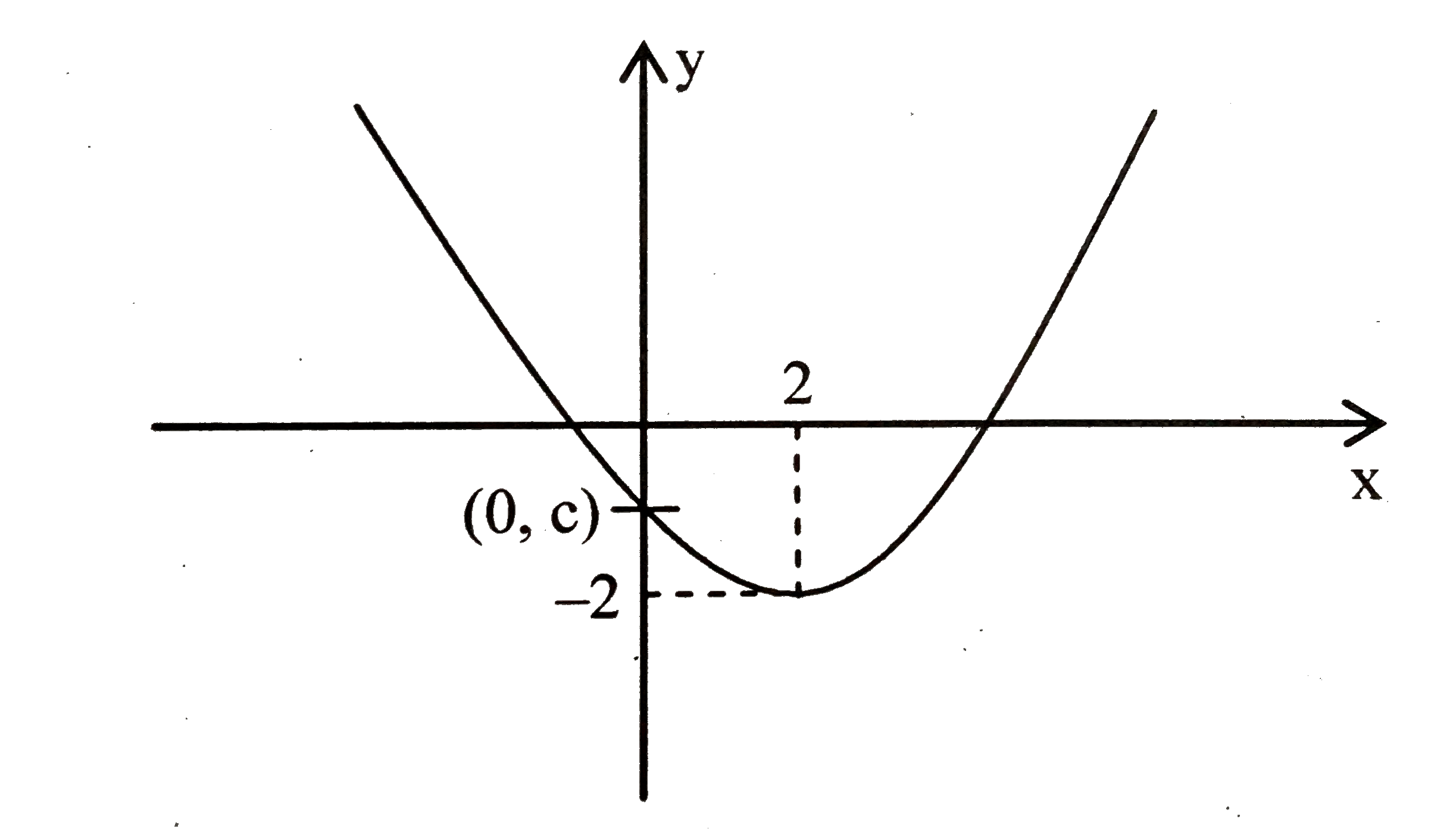



Suppose A Parabola Y Ax 2 Bx C Has Two X Intercepts One Pos



1
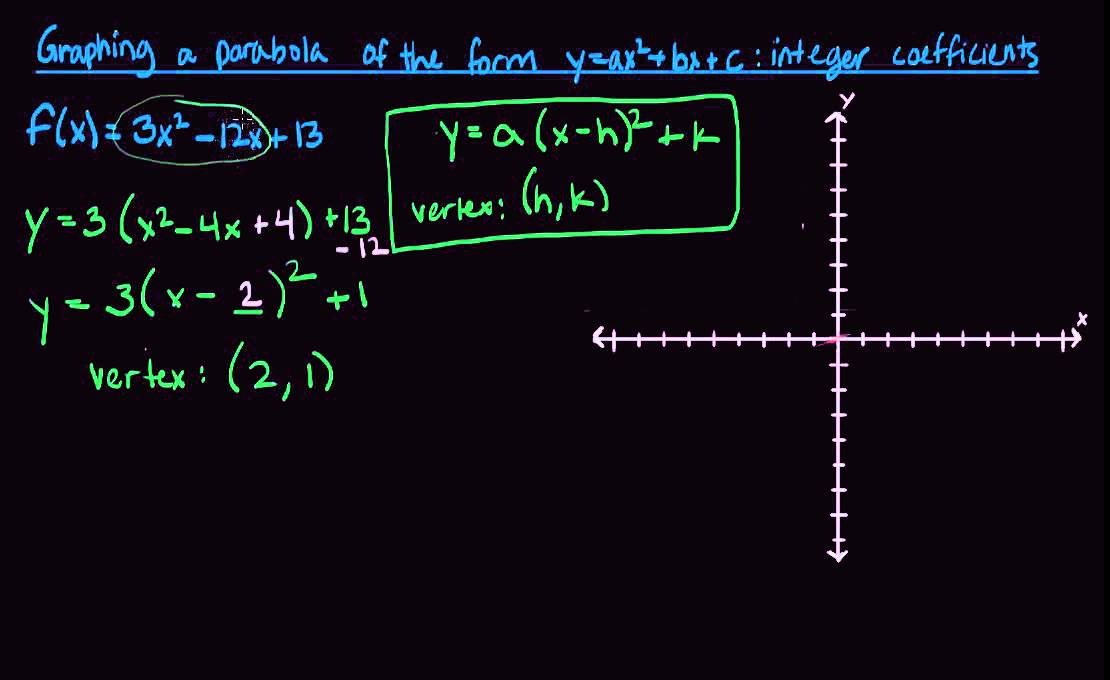



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
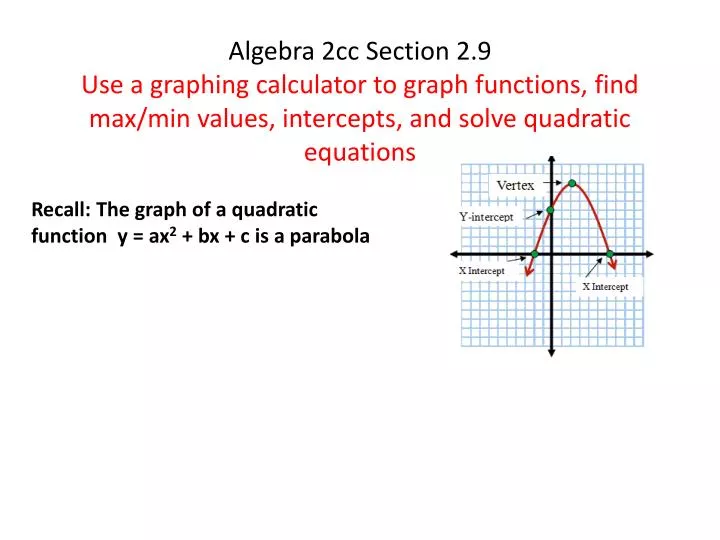



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id



Http Www Anderson5 Net Cms Lib02 Sc Centricity Domain 2152 9 1 Pdf



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora



Show That Y Ax 2 Bx C A 0 Represents A Parabola And Find Its Vertex Focus Directrix And Latus Rectum Sarthaks Econnect Largest Online Education Community
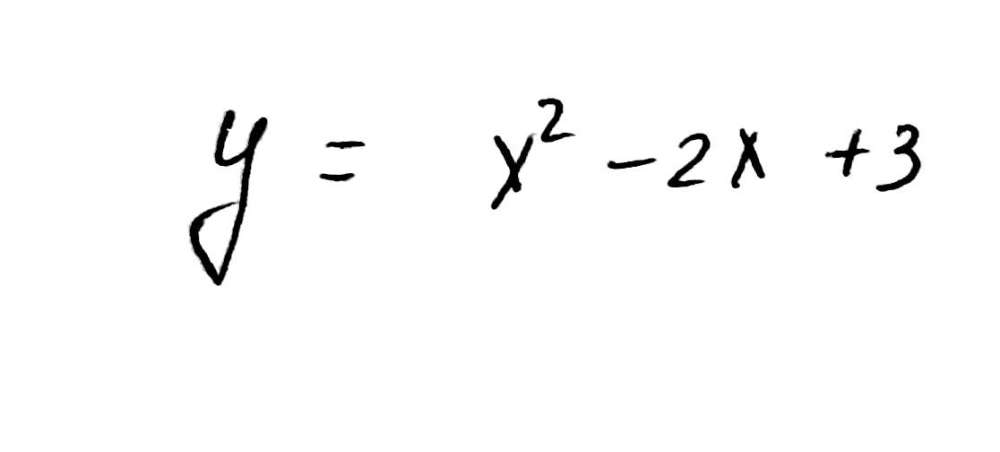



The Parabola Y Ax2 Bx C Passes Through The Points Gauthmath



Topic U2 L1 Parts Of A Quadratic Function Graphing Quadratics Y Ax 2 Bx C Eq Can I Identify The Vertex Axis Of Symmetry X And Y Intercepts Ppt Download



Math 140 Lecture 28 Y Ax2 Bx C University Of San Diego Flip Ebook Pages 1 5 Anyflip Anyflip




B Value Definition Explanation Video Lesson Transcript Study Com



Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola



Chapter 4 Quadratic Functions And Various Nonlinear Topics




Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Quadratic Equation Quadratics Parabola




Template Quadratic Function Graph Complex Roots Svg Wikipedia




Quadratic Formula Calculator



Quadratics




Parabola Y Ax2 Bx C Melalui Titik 1 2 1 6 Dan 2 3 Persamaan Parabola Tersebut Adalah Brainly Co Id



Quadratic Functions Aiming High Teacher Network



Graph Of Parabola Stock Image Image Of Lesson Presentation



Find A Parabola With Equation Y Ax2 Bx C That Chegg Com



Quadratic Function



0 件のコメント:
コメントを投稿